265. Вершинное покрытие

 

Имеется невзвешенное неориентированное дерево. Найдите такое наименьшее подмножество вершин, что для любого ребра хотя бы один из его концов принадлежит этому множеству.

 

Вход. Первая строка содержит количество вершин n (0 < n ≤ 105) в дереве. Следующие n – 1 строк задают n – 1 ребро дерева. Каждая строка содержит пару (u, v) означающую наличие ребра между вершинами u и v (1 ≤ u, v ≤ n).

 

Выход. Выведите количество вершин в искомом подмножестве.

 

Пример входа

Пример выхода

6

1 2

1 3

2 4

2 5

1 6

2

 

 

РЕШЕНИЕ

динамическое программирование

 

Анализ алгоритма

Пусть v – вершина дерева. Обозначим через:

·        dp1(v) количество вершин в требуемом наименьшем подмножестве для поддерева с корнем v при условии, что вершина v будет включена в это подмножество.

·        dp2(v) количество вершин в требуемом наименьшем подмножестве для поддерева с корнем v при условии, что вершина v не будет включена в это подмножество.

Тогда ответом задачи будет min(dp1(1), dp2(1)), если взять первую вершину за корень дерева. 

 

Определим рекурсивно приведенные функции.

·        Пусть вершина v включается во множество. Тогда сыновья вершины v можно включать, а можно и не включать во множество. Из этих двух вариантов следует выбрать тот, в котором число выбранных вершин минимально: dp1(v) = 1 + , где to1, …, tok – сыновья вершины v. Первым слагаемым стоит 1, так как вершина v включается во множество.

·        Пусть вершина v не включается во множество. Тогда сыновья вершины v необходимо включить во множество: dp2(v) = , где to1, …, tok – сыновья вершины v.

Если v – лист, то будет установлено dp1(v) = 1 и dp2(v) = 0.

 

Пример

Расставим метки dp1(v) / dp2(v) на вершинах деревьев из примеров.

 

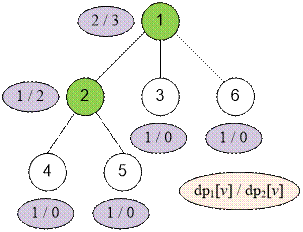
Для первой вершины:

·        dp1(1) = 1 + min(dp1(2), dp2(2)) + min(dp1(3), dp2(3)) + min(dp1(6), dp2(6))

= 1 + 1 + 0 + 0 = 2;

·        dp2(1) = dp1(2) + dp1(3) + dp1(6) = 1 + 1 + 1 = 3;

Для второй вершины:

·        dp1(2) = 1 + min(dp1(4), dp2(4)) + min(dp1(5), dp2(5)) = 1 + 0 + 0 = 1;

·        dp2(2) = dp1(4) + dp1(5) = 1 + 1 = 2;

 

Реализация алгоритма

Объявим список смежности tree для хранения дерева.

Объявим массивы dp1 и dp2.

 

vector<vector<int> > tree;

vector<int> dp1, dp2;

 

Функция dfs совершает поиск в глубину из вершины v. Предком вершины v является p.

 

void dfs(int v, int p = -1)

{

  dp1[v] = 1;

  dp2[v] = 0;

 

Перебираем ребра, исходящие из вершины v.

 

  for (int i = 0; i < tree[v].size(); i++)

  {

 

Рассматриваем ребро (v, to). Если to = p, то такое ребро не обрабатываем.

 

    int to = tree[v][i];

    if (to == p) continue;

 

Запускаем поиск в глубину из вершины to. Предком to является v.

 

    dfs(to, v);

 

Пересчитываем значения динамики.

 

    dp1[v] += min(dp1[to], dp2[to]);

    dp2[v] += dp1[to];

  }

}

 

Основная часть программы. Читаем входные данные. Строим дерево.

 

scanf("%d", &n);

tree.resize(n + 1);

for (i = 0; i < n - 1; i++)

{

  scanf("%d %d", &u, &v);

  tree[u].push_back(v);

  tree[v].push_back(u);

}

 

Запускаем поиск в глубину из вершины 1.

 

dp1.resize(n + 1); dp2.resize(n + 1);

dfs(1);

 

Вычисляем и выводим ответ.

 

res = min(dp1[1], dp2[1]);

printf("%d\n", res);